Intro

• If you prefer to mirror here is a link to the article on chain

Mathematics has always been a part of our daily lives, from simple additions to complex financial calculations. This influence extends into decentralized finance (DeFi), where numbers and equations shape the landscape.

For developers venturing into the world of decentralised finance, especially within the Solidity framework, a particular challenge arises – the subtle dance of rounding errors caused by truncation. Solidity, the language powering smart contracts on the Ethereum Virtual Machine (EVM), introduces its twists and turns when it comes to handling math, especially division.

This vulnerability was recognised by Immunefi(the top web3 bug bounty) as one of the top 10 bugs, unfortunately this was the cause of the ~$53m+ Kyberswap hack

Rounding errors are a common issue in smart contracts that involve floating-point arithmetic. These errors occur when the contracts fail to account for the limited precision or rounding in calculations, leading to potential financial discrepancies, loss of funds, or incorrect rewards.

This article unpacks the rounding errors triggered by Solidity truncation, shedding light on how these challenges play out in various math-dependent protocols. Moreover, it guides developers on steering clear of these bugs and ensuring smooth sailing in the sea of decentralised finance.

How Rounding Errors Occur

This arises due to no notion of a floating point number in solidity such that 5/10 will give 0 instead of 0.2 as opposed to other programming languages like Python or Rust due to this developers are required to implement their own using the standard integer data types this what birthed the idea of ERC20 decimals. There are several pitfalls developers can run into during this process. We will try to highlight some of these in this section.

Here are ways rounding errors occur in smart contracts

Division before multiplication

In Solidity division can result in rounding down issues, hence to minimise rounding errors we always make sure to perform multiplication before division

contract FunWithNumbers {
	uint constant public tokensPerEth = 10;
	uint constant public weiPerEth = 1e18;
	mapping(address => uint) public balances;
	
	function buyTokens() external payable {
		// convert wei to eth, then multiply by the token rate
		// @audit-issue division before multiplication
		//This will lead to rounding down
		uint tokens = msg.value/weiPerEth*tokensPerEth;
		balances[msg.sender] += tokens;
	}
	
	function sellTokens(uint tokens) public {
		require(balances[msg.sender] >= tokens);
		uint eth = tokens/tokensPerEth;
		balances[msg.sender] -= tokens;
		msg.sender.transfer(eth*weiPerEth);
	}
}

This simple token buying and selling contract has some significant limitations. Although the mathematical calculations for buying and selling tokens are correct, the lack of floating-point numbers will result in erroneous results. For instance, when buying tokens on line 8, if the value is less than 1 ether, the initial division will yield 0, resulting in an incorrect final multiplication. Similarly, when selling tokens, any number of tokens less than 10 will also yield 0 ether. Rounding is always down, so selling 29 tokens will result in 2 ether.

The main issue with this contract is that it only has the precision to the nearest ether (i.e., 1e18 wei). This can lead to problems when dealing with decimals in ERC20 tokens, where higher precision is necessary.

let's look at another example from a contest on C4 (a leading audit contest platform) This one is a bit tricky as it didn't perform any division before multiplication but doing the midst of a calculation before the calculation is completed

uint256 feePct = timeDiff * licenseFee / ONE_YEAR;
	uint256 fee = startSupply * feePct / (BASE - feePct);
	_mint(publisher, fee * (BASE - factory.ownerSplit()) / BASE);
	_mint(Ownable(address(factory)).owner(), fee * factory.ownerSplit() / BASE);

In this calculation, this will lead to precision loss as solidity truncates division operation leaving out the remainder

so the safer way to write this is

uint256 fee = startSupply * licenseFee * timeDiff / ONE_YEAR / (BASE - licenseFee);

With this, the division comes last

More examples: 1, 2, 3, 4, 5, 6, 7, 8, 9

Rounding Leaks

In most protocols, not knowing when to round up or round down can also lead to losses.

Let's try to understand rounding down and rounding up Rounding Down: Rounding down is a method of approximating a real number to the nearest, smaller integer or a specific decimal place. In this process, any fractional part of the number is disregarded, and the result is the largest integer or decimal less than or equal to the original number. For example, rounding down 4.8 to the nearest whole number would yield 4, as it is the largest integer less than 4.8.

Rounding Up: Conversely, rounding up involves approximating a real number to the nearest, larger integer or a specific decimal place. The fractional part of the number is considered, and the result is the smallest integer or decimal greater than or equal to the original number. For instance, rounding up 3.2 to the nearest whole number would result in 4, as it is the smallest integer greater than 3.2.

so how does this affect you? In the case of automated market maker (and similar) protocols rounding down will favour traders and cause leak value from the protocol. Take this sample from a finding from Cyfrin SudoSwap audit:

// @audit rounding down favours traders, can leak value from protocol
protocolFee = outputValue.mulWadDown(protocolFeeMultiplier);

from that line of code it's glaring that the protocolFee will be in favour of the traders, let's take an example where the fee = 4.9 but due to rounding down that will lead to a value leak of .9 to fix that the code needs to be changed to

// fixed: round up to favour protocol and prevent value leak to traders
protocolFee = outputValue.mulWadUp(protocolFeeMultiplier);

The Roundme repository provides a comprehensive understanding of how various mathematical operations influence the direction of rounding: rounding() is the expected rounding direction for the result (up or down)

• A + B => rounding(A), rounding(B) (addition does not change the rounding direction)

• A - B => rounding(A), ! rounding(B) (the rounding direction of the subtracted element is inverse of the expected rounding)

• A * B => rounding(A), rounding(B), rounding(*)  (multiplication does not change the rounding direction)

• A / B => rounding(A), ! rounding(B), rounding(/) (the rounding direction of the denominator is the inverse of the expected rounding)

• A ** B

  • If A>=1 => rounding(A), rounding(B)

  • If A<1 => rounding(A), ! rounding(B) (if A is below 1, the rounding direction of the exponent is the inverse of the expected rounding)

Quoting @charleswangp

Also, check this post from TaylorWebb_eth More examples 1

Unsafe Casts

When downcasting from one type to another, the Solidity compiler will not revert but overflow, resulting in an unexpected behaviour in your smart contracts which can later be exploited. Developers should make use of battle-tested libraries for safe casting such as OpenZeppelin’s SafeCast library

Take for example this line of code

// where the amount is stored in uint256
_erc20WithdrawalAllowances[_originalAddress][_erc20Address].amountStored += uint128(_amount);

This unsafe downcast will cause loss of user funds as this will cause a silent overflow and thus possible for the amount recorded to be less than the actual amount recovered. More Examples 1 2

Past Exploits

Kyberswap’s exploit as an example:

Taking this screenshot from Phalcon's analysis

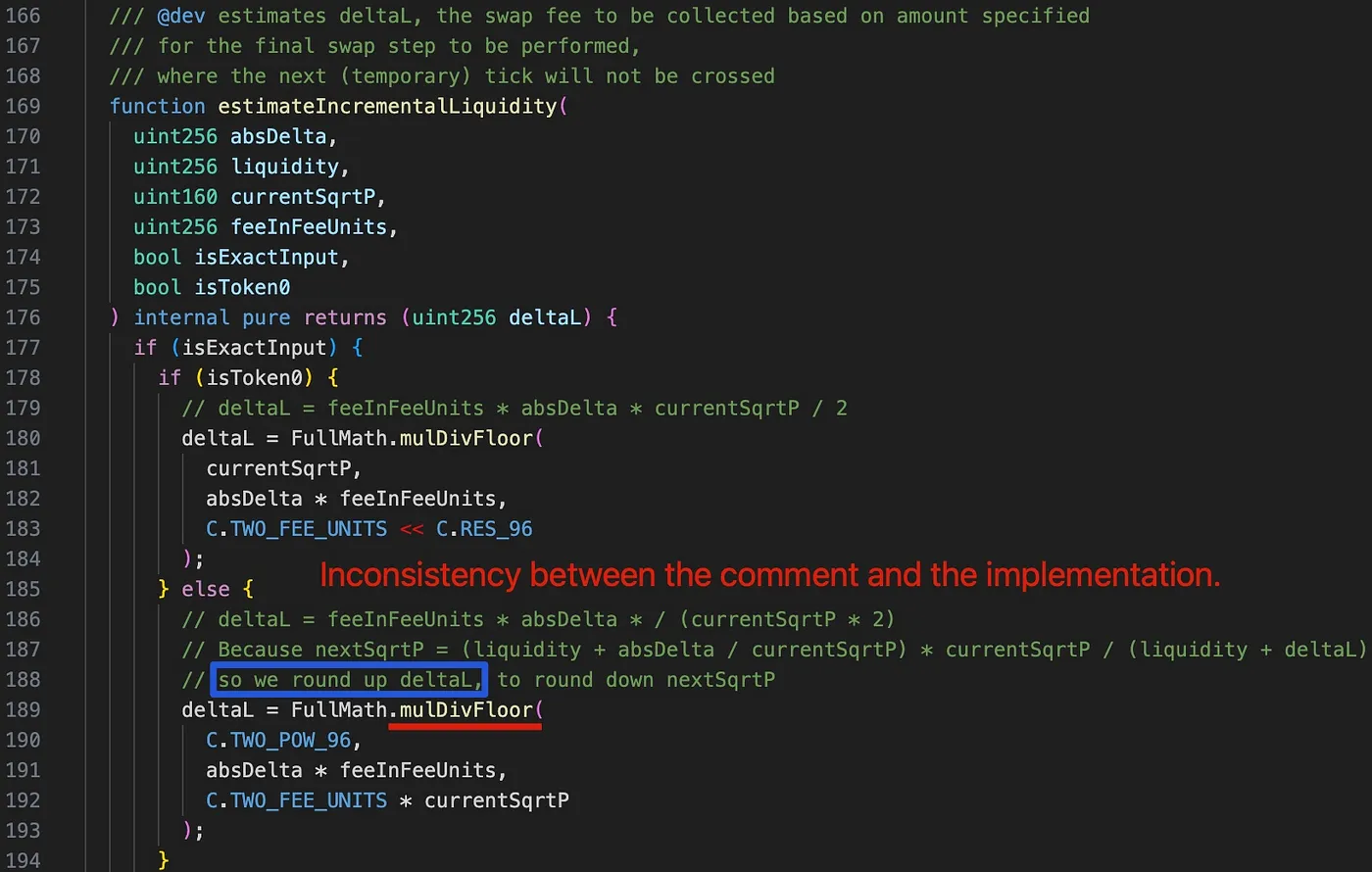
Even though the hack is specific to how kyberswap’s clamm was implemented, the root cause of the hack was because the code rounded down in favour of the user as opposed to what was written in the comment. deltaL is intended to round up in order to round down the nextSqrtP.

However, deltaL is mistakenly rounded down due to the use of the mulDivFloor function at line 189. Consequently, nextSqrtP is inaccurately rounded up.

To read more on the hack

1. Slowmist analysis

2. Phalcon analysis

HundredFinance

This exploit led to an estimated loss of $6.8 million, also in the case of this hack rounding errors in the redeemUnderlying function played a crucial role in the success of the attack.

This error is from the Compound v2 code when markets are launched with a collateral value in place but no depositors or following markets become empty due to user withdrawal post-launch. It can, however, be mitigated by:

• Minting Small cToken (or equivalent) Amounts at Market Creation Here is the official post-more and also this from Radiant Capital cream finance, OynxProtocol as they all shared the same issue plaguing compound v2 and Aave forks

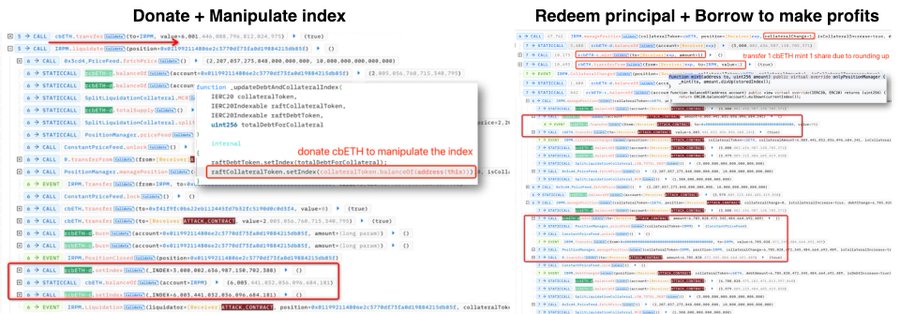
Raft finance

Also in this exploit the rounding was in favour of the user where the mint function rounds up instead of rounding down causing the attacker to receive 1 share instead of the expected 0 shares when minting. Because the index was amplified by the donation of $cbETH, the hacker's shares are worth more value, so the hacker can redeem a tiny $rcbETH-c for 6003 $cbETH and borrow tons of $R. ![[Pasted image 20240107140943.jpg]]

function divUp(uint256 a, uint256 b) internal pure returns (uint256) { 
	if (a == 0) { 
		return 0; 
	} else { 
		return (((a * ONE) - 1) / b) + 1; 
	} 
} 

function mint(
	address to, 
	uint256 amount) public virtual override onlyPositionManager { 
		_mint(to, amount.divUp(storedIndex)); 
}

Prevention Techniques

Action items

1. First, identify what each arithmetic operation does in your protocol then address when a specific operation is applied. Then make sure that operations always happen AGAINST THE FAVOR OF THE USER.

2. Consider checking the potential rounding errors in the case of rate calculation, if it is manipulative by the malicious user in edge cases, like the Raft exploit case.

3. It's recommended that when designing economic models, boundary conditions should be thoroughly tested, and liquidity and price calculations should be strictly evaluated, rather than relying on inequality checks.

Summary

In this article, I have explained how rounding errors occur and how to prevent them in your protocols as a developer.

Cheers to a more secure web3.

P.S. Want my help with your project security

you can contact me here on telegram or X,